Rainfall at a skyline

Problem Statement:

Imagine you have a list of integers representing the height of consecutive buildings (rectangles of unit width). It starts raining, and it rains until all the gaps have been completely filled with water, the excess having dripped down the sides. What is the total volume of rainfall that did not drip down the sides?

The problem is better explained with an example. For example, given the list \([4,7,1,1,5]\), we can imagine it as the following skyline:

Skyline for list \([4,7,1,1,5]\)

If rain falls, the only place where the rain will stay is between the second and fifth building, for a total of 8 units of rain. We need to come up with an algorithm that can compute this value.

Consider a building \(b\) of height \(h\). We need to figure out how much water will stay atop of this building after rainfall. This is dependent on the buildings to the left and right of \(b\) - if there is to be any water at all atop of \(b\), then the there must be buildings to the left and right of \(b\), both with height higher than \(h\). Otherwise, no water would stay atop of \(b\) as it would flow out one of the sides. This leads us to the idea that the amount of water that gathers on \(b\) is related to the buildings with maximal height to the left and right of \(b\). Consider the following scenario, the building with an arrow as building \(b\).

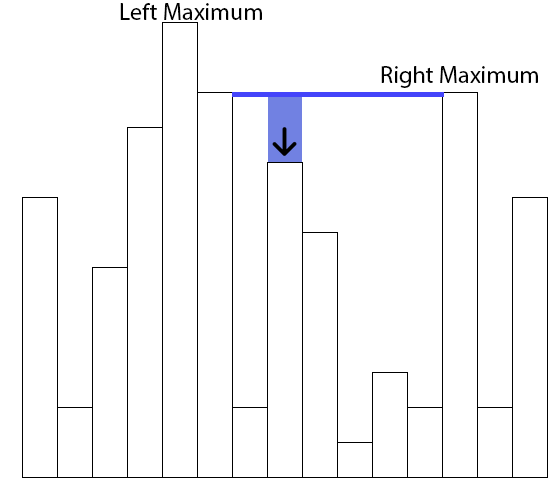
The amount of water on top of the building with the arrow is related to the height of the smaller of the highest buildings to the left and right of the marked building.

Call the marked building \(b\) (height \(h\)), the building to the left of \(b\) with maximal height \(h_l\), \(b_l\), and the building to the right of \(b\) with maximal height \(h_r\), \(b_r\). The water that deposits on top of \(b\) is then \(\operatorname{min}(h_r,h_l) - h\).

The total amount of rain is then:

\[\sum_{b} (\operatorname{min}(\operatorname{maxheight(left(b))},\operatorname{maxheight(right(b))}) - h)\]

which we can directly translate to a Python program:

def solveInefficient(skyline):
  flow = 0

  for i in range(0,len(skyline)):
    leftSublist   = skyline[0:i+1]
    rightSublist  = skyline[i:len(skyline)]

    maxL = max(leftSublist)
    maxR = max(rightSublist)

    minMax = min(maxL,maxR)
    
    flow += minMax - skyline[i]

  return flow

The algorithm is correct, but inefficient. For every element, we compute the maximum to the left and to the right. The algorithm hence has quadratic complexity in the number of buildings. We can improve this to linear time by precomputing the highest buildings to the left and right of every building:

Make two passes through the list of integers representing the heights of the buildings. Do the first pass left to right, and keep the highest element seen so far. Do the second pass from the right, and again, keep the highest element seen so far. Now, for any element, we have the highest elements both to the left and right of the element. The improved linear algorithm is then:

def solveEfficient(skyline):
  # Initialize two arrays
  maxFromLeft  = [skyline[0]] + [None for i in range(len(skyline)-1)]
  maxFromRight = [None for i in range(len(skyline)-1)] + [skyline[len(skyline)-1]]

  for i in range(1,len(skyline)):
    # Update the maximum values seen so far
    maxFromLeft[i] = max(skyline[i],maxFromLeft[i-1])
    maxFromRight[len(skyline)-i-1] = max(skyline[len(skyline)-i-1], maxFromRight[len(skyline)-i])

  # Get the minimum values
  mins = map(min,zip(maxFromLeft,maxFromRight))

  return sum( [ minHeight - height for (height,minHeight) in zip(skyline,mins)] )

For the picture in this post, both algorithms give the correct answer 56.